Алгоритм Ванга-Ландау приобретает актуальность и активно применяется для исследования фазовых переходов в сложных спиновых системах, спиновых стеклах. Метод интересен в первую очередь потому как позволяет преодолеть эффект критического замедления.
Данный метод представляет интерес в первую очередь вследствие того, что позволяет преодолеть эффект критического замедления, который возникает вблизи температуры фазового перехода и существенно увеличивает время моделирования традиционными методами Монте-Карло. Алгоритм Ванга-Ландау позволяет, единожды вычислив плотность энергетических состояний системы, получить такие термодинамические величины как внутренняя энергия, теплоемкость, свободная энергия, энтропия. Существует ограничение, которое связано с расходимостью (гистограмма посещений никогда не становится плоской) данного метода для решеток больших размеров, что приводит к сложностям в моделировании трехмерных систем и больших двумерных решеток, которые связаны с большим или неопределенным временем моделирования.
Основные понятия, используемые в алгоритме, описанным блок-схемой на рис.1: H(E) – вспомогательная гистограмма, отражает количество посещений каждого энергетического уровня. M — некоторое большое число, например 104. f — фактор, используемый в алгоритме. Процесс инициализации состоит из нескольких шагов:
- так как начальное значение g(E) неизвестно, то присваивается g(E) = 1 для всех значений E;
- Устанавливается начальное значение вспомогательной гистограммы H(E)=0 для всех состояний с энергией E;
- Задается начальное значение спинов si = 1 или si = -1;
- Фиксируется начальное значение параметра f = 2.71828182846;
Алгоритм Ванга-Ландау состоит в следующем:
- Случайно выбирается спин si;
- Вычисляется энергия решетки до трансформации E1 и после E2 (под трансформацией будем понимать смену знака у si);
- Вероятность принятия нового состояния вычисляется по формуле p(E1->E2) = min(E1 /E2 , 1). Это означает, что если g(E2) < g(E1), то новое состояние принимается, если нет, то принимается с вероятностью g(E1) /g(E2). После принятия нового состояния E2:
(a) Изменяется значение вспомогательной гистограммы H(E2) H(E2) + 1;
(b) Обновляется соответствующее значение плотности состояния путем умножения на фактор f g(E2) ->g(E2)*f;
(c) Переворачивается спин;
- Если новое состояние не принято, то
(a) Изменяется и g(E1)-> g(E1)*f
(b) Обновляется гистограмма H(E1) ->H(E1) + 1
- Пункты 1-4 повторяются MN-раз, N — количество спинов на решетке;
- Гистограмма H(E) проверяется на «ровность». В алгоритме под «ровностью» предполагается, что H(E) для всех состояний отличается не более, чем на 5% от среднего <H(E)>.
- Если гистограмма имеет желаемый уровень «ровности» то:
(a) Выполняется нормировка плотности состояния g(E) для всех E на единицу значения плотности состояния энергии основного состояния моделируемой системы;
(b) Устанавливается значение гистограммы H(E)=0 для всех E;
(c) Изменяется значение параметра f =$$\sqrt f$$ ;
- Если гистограмма H(E) не достаточно «ровная» то пункты 1-6 повторяются еще MN-раз;
- Шаги 1-8 повторяются, пока значение не будет меньше, чем f=1.000000001
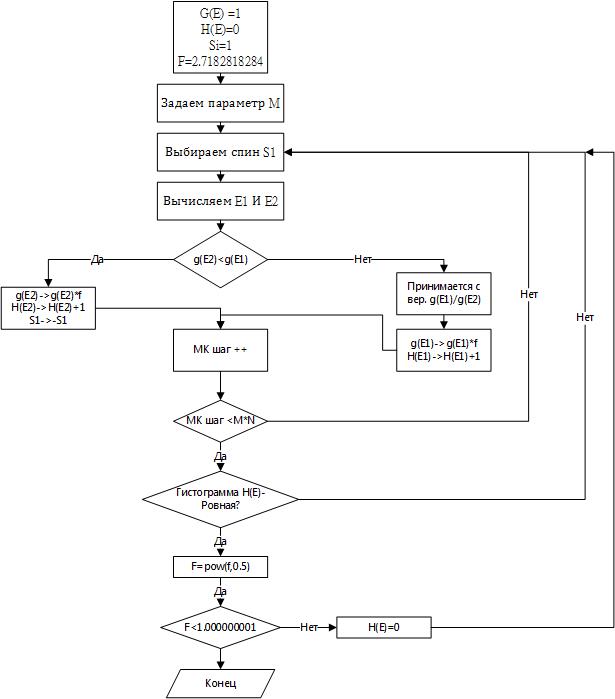
Рис. 1. – Блок-схема алгоритма Ванга-Ландау
Параллельный алгоритм Ванга-Ландау
При использовании алгоритма Ванга-Ландау для решеток больших размеров появляется ограничение, связанное с расходимостью, (т.е. гистограмма посещений энергетических уровней никогда не становится плоской). В связи с этим увеличивается время моделирования трехмерных и больших двумерных решеток. Можно преодолеть данное ограничение путем параллелизации алгоритма разделением энергетического интервала на подчасти, каждая из которых будет выполняться отдельной копией алгоритма (рис. 2). Между данными параллельными репликами алгоритма будет происходить обмен информацией для соблюдения баланса. Главная задача параллельного алгоритма состоит в уменьшении размера обрабатываемого пространства, отсюда последует лучшая сходимость гистограммы для каждой реплики и уменьшится время моделирования.
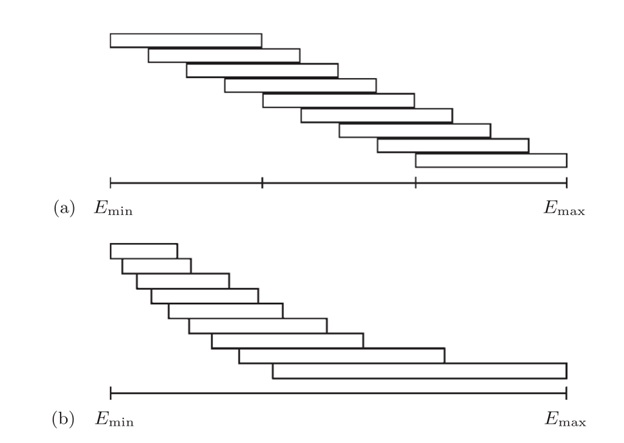
Рис. 2. – Варианты разбиения энергетического интервала на части а) на равные б) с различным коэффициентом перекрытия и динамической балансировкой.
Отличие параллельного алгоритма Ванга-Ландау от последовательной состоит в том, что общий энергетический интервал разбивается на части, в результате чего отдельные зоны обрабатываются параллельно [24]. После определенного количества Монте-Карло шагов осуществляется обмен энергетическими состояниями между репликами внутри пересекающегося интервала с вероятностью ½. Помимо этого, для сохранения баланса между репликами на каждом шаге происходит обмен с вероятностью
$$P_{ex}=min \left[1, \frac{g_i(E(C_x)) g_j(E(C_y))}{g_i(E(C_y)) g_j(E(C_x))}\right]$$
С данной вероятностью происходит увеличение значения плотностей энергетических состояний и гистограмм для данных состояний. После того, как все энергетические зоны будут иметь «плоские» гистограммы, происходит их усреднение и перераспределение плотностей энергетических состояний для всех реплик. На каждом шаге алгоритма полученные гистограммы должны обнуляться.
При помощи данного метода для двумерной модели Изинга были получены результаты, которые совпадают с результатами, полученными в ходе последовательного алгоритма. Сравнить результаты можно по основной вычисляемой величине – плотности энергетических состояний, из которой можно получить все термодинамические характеристики (Рис. 3).
На рисунке 3 видно, что отклонение полученных результатов от последовательной версии алгоритма минимально, но в то же время наблюдается накопление систематической ошибки с увеличением числа потоков.
Параллельный алгоритм Ванга-Ландау может быть успешно применен и к трехмерной модели Изинга.
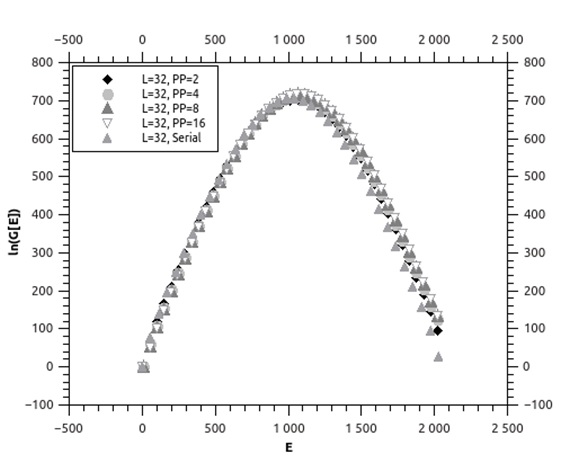
Рис. 3. – Плотность энергетических состояний, полученная для двумерной модели Изинга с размером решетки L=32 при распределении на разное количество потоков PP=2,4,8,16 в сравнении с последовательной версией
График теплоемкости (рис. 4) трехмерной модели показывает, что для параллельной версии получаемая теплоемкость имеет пик в точке фазового перехода второго рода и согласуется с данными, полученными другими методами, такими как алгоритм Метрополиса, кластерные алгоритмы Вольфа и Свендсена-Ванга.
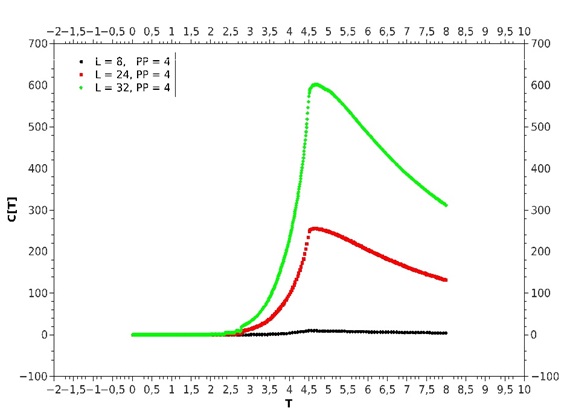
Рис.4. – График теплоемкости для трехмерной модели Изинга, полученный алгоритмом Ванга-Ландау для решеток размера L = 8, 24, 32 при разделении энергетического интервала на 4 подчасти.

