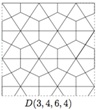
Вариант №1
1. Изучить исходный код примера (wl_diluted_ising_triangular_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
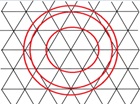
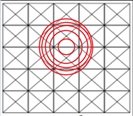
На рисунке приведена треугольная решетка, и обозначены три координационные окружности (окружности проходят через вершины, соседствующие с центральной вершиной)
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки. Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла треугольной («triangular», см. выше) решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая окружность, n3[] – третья и т.д. (для каждого типа совокупностей расстояний).
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь то же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси OX равно nx, по оси OX равно nу.
Вариант №2
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка кагоми. Окружности проходят через узлы, т.е. через вершины графа, и приведены пять координационных сфер (окружности включают себя узлы, соседствующие с центральным).
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки. Примеры нумерации вершин:

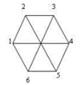
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки кагоми в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. (для каждого типа совокупностей расстояний).
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В \textit{первом} файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь то же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
\vspace{1cm}
Вариант №3
1. Изучить исходный код примера (wl_diluted_ising_triangular_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
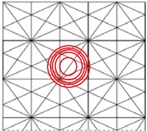
На рисунке приведена треугольная решетка и
обозначены пять координационных окружностей (окружности
проходят через центры ребер).
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки. Примеры нумерации вершин:


3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла треугольной («triangular», см. выше) решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая окружность, n3[] – третья и т.д. (для каждого типа совокупностей расстояний).
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь то же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №4
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).

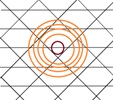
На рисунке приведена решетка дуальная к решетке кагоми.
Окружности проходят через центры ребер,
приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки. Примеры нумерации вершин:


3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки дуальной к решетке кагоми в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. (для каждого типа совокупностей расстояний).
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь то же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №5
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка пенроуза. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки.
Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь то же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №6
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
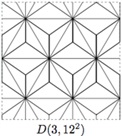
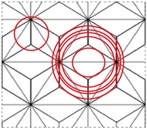
На рисунке приведена разновидность решетки пенроуза. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки. Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь тот же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №7
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки.
Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь тот же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №8
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки.
Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь тот же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №9
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки.
Примеры нумерации вершин:
3.3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь тот же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
Втретьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.
Вариант №10
1. Изучить исходный код примера (wl_diluted_ising_kagomi_modified.c), скомпилировать и запустить его на кластере ДВФУ (cluster.dvfu.ru).
На рисунке приведена решетка. Приведены пять координационных окружностей.
2. Вычислить радиусы 5ти координационных окружностей (если совокупность расстояний отличается для ребер графа различной длины, вычислить все возможные расстояния) при условии, что параметр решетки равен a. Нарисовать решетку, дуальную данной в редакторе векторной графики, рисунок сохранить в формате pdf или eps. Пронумеровать вершины графа дуальной решетки, изобразить и подписать радиусы окружностей (сфер), обозначить параметр решетки.
Примеры нумерации вершин:
3. Разработать алгоритм, и реализовать функцию period() в виде Си кода для вычисления соседей каждого узла решетки в 1й, 2й, 3й, 4й и 5й координационных окружностях. Соседи (номера узлов или вершин графа) из каждой координационной окружности должны храниться в виде отдельных массивов, названия которых n1[] -первая координационная окружность, n2[] – вторая, n3[] – третья и т.д. Кроме того, отдельно необходимо выделить соседей, дуальной решетки к указанной выше, расположенных на длинных отрезках.
4. Оформить вывод функции period() в виде трех отдельных файлов *.dat, необходимых для проверки правильности расчетов и визуализации полученных данных.
В первом файле должны содержаться построчно: номер узла, соседи из первой координационной окружности, из второй и т.д. с учетом свободных граничных условий. Отдельно оформить вывод вершин дуальной решетки (центров), находящихся на длинных ребрах графа.
Например,
Node \#1
2, 3, 7, 8
4, 5, 2,9
10, 11, 12,
…
Второй файл должен иметь тот же самый формат, что и первый файл, только данные должны быть получены с учетом периодических граничных условий.
В третьем файле должна содержаться информация в формате, пригодном для передачи в сторонний программный пакет (Mathematica, Matlab, Simulink, Graphviz, или любой другой выбранный вами для визуализации) т.е. читабельные выбранным вами пакетом данные, необходимые для построения графа (без учета граничных условий), т.е. данные для визуализации решетки.
5. Реализовать возможность визуализации решетки для произвольных параметров nx и ny для плоской решетки. Функция period() должна позволять масштабирование решетки для общего числа узлов nla=nx*ny, с учетом того, что число узлов по оси 0x равно nx, по оси 0у равно nу.