Параллельный алгоритм Метрополиса. Подход №2.
В данной лабораторной работе с использованием MPI необходимо реализовать вариант параллельного алгоритма Метрополиса, состоящий в декомпозиции матрицы спинов по процессам.
Параллелизм алгоритма реализуется за счет разбиения массива спинов на части, последующей их рассылки посредством MPI библиотеки и, соответственно, обработки каждой из частей в отдельном вычислительном процессе. Проход по системе спинов и выполнение Монте-Карло шагов в алгоритме Метрополиса производятся в «шахматном порядке». Это делается с целью решения задачи о граничных условиях вычисляемых конфигураций для обрабатываемых плоскостей, см. рисунок 1.
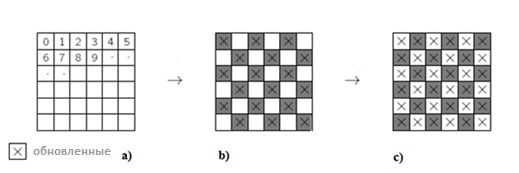
В течении МК операций с частью массива, первоначальные значения соседей обрабатываемого спина не изменяются, т.е. в данном случае, для каждого шага температуры или поля, половина МК шагов делается сначала для одной половины спинов (рис 1(b), а затем для второй половины (рис1 (c).
1) В каждый процесс сообщаются данные о числе строк массива со спинами. Число строк пропорционально количеству процессов.
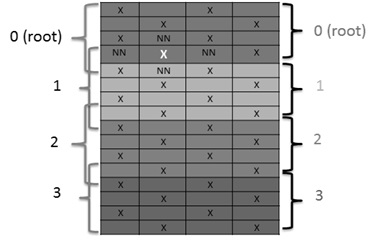
2) Для учета ближайшего окружения спинов магнетика, стоящих на границе блоков строк, в каждый процесс направлялись дополнительные строки, содержащие спины на границе строки, см. рисунок 2;
3) Рассылка блоков строк осуществляется с помощью in-line функции коллективного обмена данными MPI_Scatterv — рассылающей части неодинаковой длины из root-процесса в другие процессы, а сборка в один массив в процессе root осуществляется с помощью функции MPI_Gatherv. Использование данных функций MPI позволяет рассылать по процессам блоки данных различных размеров, см. рисунок 2, так как кроме «основных» блоков данных, которые ограниченны фигурными скобками справа, необходимо в каждый процесс отправлять дополнительные строки, содержащие ближайших соседей (NN), размер «расширенных» блоков различен, эти блоки выделены фигурными скобками слева.
4) Поиск равновесной конфигурации производится параллельным методом Монте-Карло с помощью MPI функции MPI_Reduce с использованием операции MP_MIN, которая позволяет из множества сгенерированных конфигураций выбрать конфигурацию, которой соответствует минимум энергии. Данная конфигурация становится стартовой для нового цикла Монте-Карло для всех процессов при следующем значении температуры или внешнего поля. В программе эта возможность реализована таким образом, что возможно в параллельном режиме, одновременно генерировать неограниченное количество процессов для поиска равновесной конфигурации, обладающей минимумом энергии. Также использована функция MPI_Comm_group, с помощью которой генерируются группы процессов и в каждой из них независимо осуществляется поиск конфигурации с минимумом энергии, а затем с помощью интеркоммуникаторов осуществляется обмен и поиск конфигурации обладающей минимумом свободной энергии.

