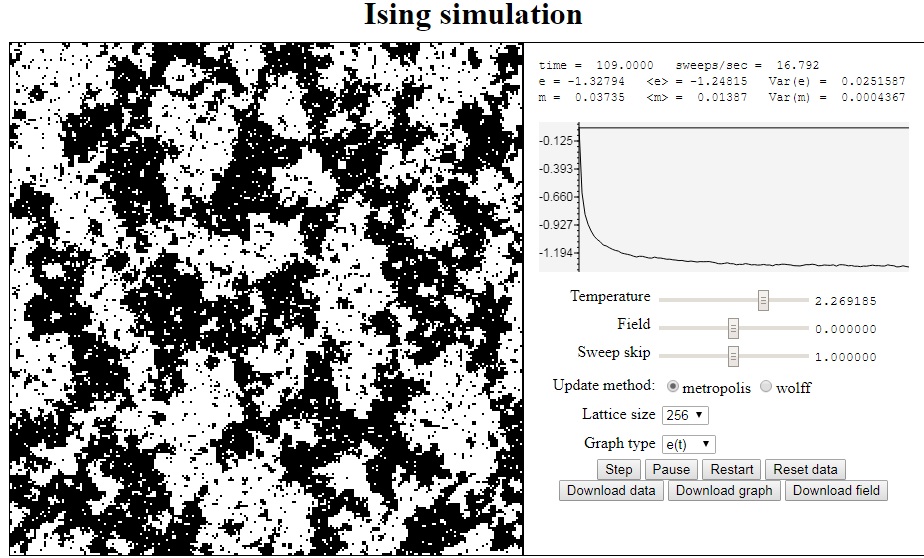
Алгоритм Метрополиса считается самым успешным среди остальных методов Монте-Карло. Узнай, почему.
Работы, связанные с этим алгоритмом, составляют целую область науки, содержащей обширную теорию и созданные приложения на тему физического моделирования. Алгоритм Метрополиса обладает хорошей масштабируемости при параллельных вычислениях и возможностью повышения точности вычислений. Важной характеристикой алгоритма Метрополиса для задачи Изинга является корреляционное время τ. Вычисляемые величины обычно после достижения теплового равновесия усредняются по конфигурациям, разделенным между собой заданным числом шагов Монте-Карло, равное больше, чем τ. В динамике поведения спиновых систем наблюдаются сильные корреляции, особенно сильно проявляющиеся вблизи критической температуры. Это явление называется критическим замедлением. Корреляционное время τ вблизи критической точки расходится по степенному закону \( \tau \sim|T-T_c|^{-vz}\), где z – динамический критический индекс. Для рассматриваемого алгоритма Метрополиса динамический критический показатель z ≈ 2 и почти не зависит от размерности задачи.
Для двумерной модели Изинга v =1 и при T=Tc, когда корреляционная длина сопоставима с размером решетки ξ~L, расходимость имеет приблизительно квадратичный характер, то есть \(\tau\)(Tc) ~L2. Подобное поведение затрудняет использование алгоритма Метрополиса для больших систем вблизи критической точки (вблизи фазового перехода). Кроме того, его применение не всегда ведёт к ответу на вопрос о типе фазового перехода, т. е. дифференциации фазового перехода первого и второго рода.
Существует ряд алгоритмов, позволяющих преодолеть проблему критического замедления. К ним относятся кластерные алгоритмы Монте-Карло.
Алгоритм Метрополиса состоит в следующем (рис. ): вычисляется энергия «старой» конфигурации E1 и «новой» Е2. Энергия «новой» конфигурации сравнивается с энергией «старой» конфигурации. «Новая» конфигурация принимается и становится исходной для следующего шага, если Е1>Е2, в противном случае рассчитывается вероятность переворота данного спина р(Е1→Е2):
$$
p(E_1 \rightarrow E_2)= \left \{ \begin{aligned}
1 \text{, если} E_1>E_2 \\
e^\frac{E_2-E_1}{T} \text {, если} E_2\leq E_1\end{aligned}
\right \}
$$
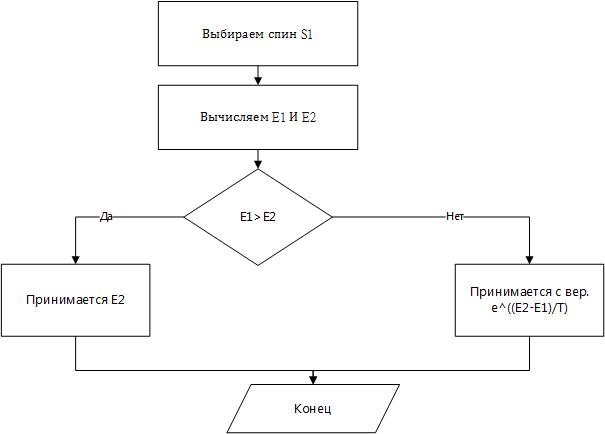
Рис. – Блок-схема алгоритма Метрополис
Начальное состояние может быть далеким от равновесного. Алгоритм Метрополиса обеспечивает сходимость состояний к равновесному за разумное число шагов, и нет необходимости изучать все 2N состояний, как правило достаточно приблизительно 10N итераций. В принципе, состояния можно было бы разыгрывать другим способом, например, сразу используя распределение Гиббса, и должен получаться правильный результат, но для этого потребуется больше вычислительного времени. В этом и заключается преимущество алгоритма Метрополиса.
Перейдя по ссылке Моделирование модели Изинга, можно наблюдать модель в динамике, самостоятельно изменяя параметры.