Что называется моделью? Для чего необходима модель? Какие бывают компьютерные модели? Что такое вычислительный эксперимент?
1. Модель и ее назначение
2. Классификация компьютерных моделей
3. Вычислительный эксперимент
1. Модель и ее назначение
Моделью называется объект, который заменяет реальный предмет или явление для изучения его свойств. Модель называют инструментом познания объекта.
Известно, что, правильно построенная модель информативнее и доступнее при изучении свойств, чем реальный объект. Существует несколько требований к модели, после выполнения которых модель можно считать информативной. К ним относятся:
наглядность и видимость основных свойств и построения;
доступность ее для исследования или воспроизведения;
простота исследования, воспроизведения;
сохранение информации, содержащейся в оригинале и способность получение новой информации.
Для того, чтобы результаты моделирования можно было использовать при работе с реальным объектом, модель должна быть адекватной, то есть свойства модели должны совпадать со свойствами реального объекта. Смысл замены реального объекта для исследования его моделью в том, что исследовать модель дешевле и проще, к тому же в некоторых случаях безопаснее.
Модель отражает наиболее значимые свойства объекта, оставляя без внимания второстепенными.
К основному предназначению моделирования можно отнести изучение поведения сложных систем физических процессов и явлений. Некоторые объекты и явления не могут быть изучены естественным образом ввиду различных факторов. В других случаях, исследования компьютерных моделей могут предшествовать реальным экспериментам для оценки необходимых ресурсов.
Естественно, модель любого реального явления или объекта недостаточно точна, нежели само явление или объект, но хорошо построенная модель способна отобразить все свойства и нюансы поведения системы в целом. Благодаря отображению всех характеристик объекта разом.
Модель способна научить надлежащим образом управлять реальным объектом путем проб и ошибок. Использовать для этой цели реальный объект бывает невозможно либо рискованно и неоправданно.
Итак, модель необходима для:
изучения структуры реального объекта, его свойств, законов взаимодействия с внешней средой;
обучения управлению явлением или объектом;
предсказаний поведения и состояний объекта при изменяющихся условиях.
Если классифицировать модели по способу реализации, то они бывают абстрактными и материальными. Абстрактную модель можно назвать мысленной, она находится только в нашем воображении. Примером могут быть алгоритмы, которые можно представить в виде блок—схемы. Материальные или физические модели представляют собой макеты или устройства, имеющие функции и свойства изучаемого объекта, над которыми в процессе исследования проводится ряд экспериментов. Например, модель двигателя автомобиля или уменьшенная точная модель подводной лодки.
Модели можно разделить на вербальные, математические и компьютерные. Вербальные модели представляют собой утверждения, записанные на естественном или формализованном языке, которые описывают изучаемый объект. Математические модели представляют собой совокупность математических операторов и действий с ними, часто это есть система уравнений. Компьютерная модель это программа или их совокупность, которая благодаря математическим преобразованиям имитирует поведение изучаемой системы.
2. Классификация компьютерных моделей
Одним из эффективных способов изучения явлений является научный эксперимент, то есть воспроизведение изучаемого явления в контролируемых условиях, которыми можно управлять. Исследуемый объект часто заменяют компьютерной моделью ввиду большей удобности и экономичности. Благодаря распространению мощных ЭВМ и информационных технологий в настоящее время компьютерное моделирование можно назвать самым результативным методом исследования физических, технических и других систем. Компьютерные модели позволяют выявить основные условия, которые определяют свойства изучаемых явлений и объектов, изучить обратную связь системы на изменяющиеся условия.
Компьютерная модель – это отдельная программа либо программный комплекс, которые позволяют при помощи вычислений и графического отображения результатов воспроизводить реальные объекты и процессы при воздействии на них различных факторов. Такие модели еще называют имитационными.
Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе изучения ее компьютерной модели. Смысл такого моделирования состоит в получении количественных и качественных результатов по созданной модели, что позволяет изучить неизвестные ранее свойства системы. Компьютерная модель должна отображать максимальное количество взаимосвязей и характеристик реального объекта, существующие ограничения. Модель следует строить универсальной, чтобы использовать ее для описания подобных объектов; простой, чтобы обойтись разумными тратами на исследование.
Компьютерная модель также является отличным наглядным и обучающим пособием для учащихся. При использовании компьютерной модели в качестве обучающего механизма существуют возможности:
- рассмотреть сложные явления и процессы на доступном уровне;
- сделать акцент на главных свойствах системы благодаря гибкой форме ее представления и наличию эффектов мультимедиа;
- наблюдать за процессом в динамике, учитывая все его изменения;
- представлять работу системы в наглядном виде: графики, схемы, диаграммы;
- предпринимать действия невозможные в реальности из-за пространственно-временных рамок или опасения за безопасность модели и окружающей среды.
Виды компьютерных моделей.
Для начала определимся, каким может быть компьютерное моделирование.
- Физическое моделирование – моделирование, при котором создается целая установка для проведения экспериментов либо отдельный тренажер, например, для тренировки управления самолетом. Такая модель принимает внешние сигналы, осуществляет необходимые математические операции и выдает соответствующие сигналы для управления моделью.
- Численное моделирование – решение системы уравнений математическими методами, проведение вычислительного эксперимента на основе входных параметров системы и внешних воздействий на нее. Примером может служить моделирование любых природных и искусственных процессов.
- Суть имитационного моделирования в создании программы, которая будет имитировать поведение сложной системы. Такая имитация основана на формальном описании логики существования системы, при котором учитываются взаимодействия всех ее составляющих. Примерами являются исследования биологических, физических и других систем, а также создание игр, обучающих программ.
- Информационное моделирование – создание информационной модели, то есть объединенных вместе данных, классифицированных по определенным признакам, определяющих суть исследуемого объекта. Информационной моделью являются таблицы, графики, анимации, диаграммы, карты.
- Моделирование знаний, к которому относится создание систем искусственного интеллекта. За основу таких моделей берутся знания какой-либо области, состоящие из данных и правил. Примером служат экспертные системы, логические игры, программы для роботов, создания эффектов виртуальной реальности и прочее.
Исходя из всего вышеперечисленного, компьютерные модели можно разделить на:
- дискриптивные модели, описывающие исследуемый объект и факторы, влияющие на изменения в его поведении.
- оптимизационные модели помогают определить наиболее подходящий способ взаимодействия со сложной системой, управления ею.
- прогностические модели предсказывают состояние объекта в конкретные моменты в будущем.
- учебные модели, используемые для наглядного обучения обучающихся, их тестирования.
- игровые модели создают несуществующие ситуации, имитирующие реальность, играют в логические игры.
Под компьютерным моделированием изначально подразумевалось только имитационное моделирование, однако, не трудно заметить, что использование компьютера для других целей может значительно помочь для решения поставленных задач. Например, построение современных математических моделей по входным экспериментальным данным невозможно или труднодостижимо без использования компьютера.
Первые задач, решаемые с помощью компьютерного моделирования, были связаны с физикой и представляли собой в основном сложные нелинейные задачи физики с помощью итерационных схем и по сути являлось математическим моделированием. Хорошие результаты в моделировании в области физики распространили использование этого метода исследования и на другие области. Сложность решаемых моделированием задач зависела только от мощности используемых компьютеров, тем самым и ограничивалась несовершенными мощностями
После публикации в 1948 году статьи Дж. Неймана и С. Улама, в которой впервые было описано применение метода Монте-Карло, многие исследователи стали называть компьютерное моделирование методами Монте-Карло. Это не верно, правильней будет выглядеть разделение компьютерного моделирования на несколько направлений[6]:
- Методы Монте-Карло или методы вычислительной математики. Используются численные методы, объекты заменяются числами, результаты формируются в таблицы или графики;
- Методы имитационного моделирования;
- Методы статистической обработки данных на основе метода планирования эксперимента;
- Комплексы имитационного моделирования, в которых объединяются все вышеупомянутые методы.
Разновидностью компьютерного моделирования является вычислительный эксперимент, который предполагает дальнейшее численное исследование модели после ее создания, позволяющее исследовать объект в различных его модификациях и при различных условиях.
3. Вычислительный эксперимент
С использованием ЭВМ для выполнения арифметических и логических операций производительность интеллектуального труда человека значительно возросла. Первые задачи, для которых создавались ЭВМ, были связаны с ядерной энергией и освоением пространства космоса. Сейчас же компьютер принимает участие в различных задачах и исследованиях, эта технология теоретических экспериментов получила название вычислительного эксперимента. Основой вычислительного эксперимента является математическое моделирование, теоретической базой – прикладная математика, а технической – мощные электронные вычислительные машины.
Компьютерное моделирование и вычислительный эксперимент становятся новым методом научного познания для исследования сложных моделей систем. Цикл вычислительного эксперимента принято разделять на несколько этапов для лучшего восприятия сути этого метода.
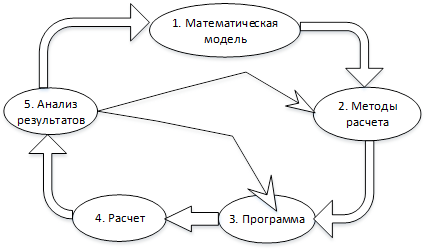
Цикл вычислительного эксперимента
- Построение математической модели. Одновременно происходит и формулировка допущений, в которых результаты будут реальными для этой модели. Математическая модель, как правило, представляет собой дифференциальные или интегральные уравнения.
- Выбор численных методов расчета. Эти методы есть совокупность последовательностей математических формул, по которым следует проводить вычисления. Необходимое условие – вычислительные методы должны быть эффективными, чтобы получить точное решение с минимальными затратами времени и ресурсов.
- Создание программы, реализующей вычислительный алгоритм.
- Проведение расчетов и обработка полученной информации.
- Анализ результатов расчетов, сравнение с натуральным экспериментом (при возможности). Результаты этого этапа могут быть двух видов: появляется необходимость пересмотра модели и ее уточнения либо полученные расчеты проходят проверку на адекватность и эксперимент считается завершенным. Чаще всего возникает необходимость корректировки созданной модели, изменения численных методов и программы. Таким образом, происходит усовершенствование алгоритма, уточнение математической модели.