Для описания системы необходимо найти статистическую сумму, в которой содержится полная информация о всех состояниях системы. Другие характеристики системы: внутренняя энергия, энтропия, свободная энергия вычисляются через статистическую сумму или ее производные. Необходимо заметить, что количество членов статистической суммы экспоненциально растет с увеличением числа частиц, соответственно увеличивается и время расчета термодинамических параметров для большого количества частиц. Поэтому при исследовании спиновых систем стали использоваться различные вероятностные численные методы. Для этого реальная система заменяется некоторой идеальной системой – моделью. В математическом виде указываются состояния s и вид энергетической функции Гамильтона E(s).
Гамильтониан одномерной цепочки из N спинов, каждый из которых взаимодействует только с двумя ближайшими соседними спинами:
$$ \hat{H}=-\sum_{i=1}^{N=1} J_i\sigma_i \sigma_{i+1}, \sigma_i =\pm1$$
Цель расчета – получить статсумму для этой цепочки.
$$Z_N=-\sum_{\sigma_1=-1}^{+1}\sum_{\sigma_2=-1}^{+1}…\sum_{S_n=-1}^{+1} exp\left(\beta\sum_{i=1}^{N-1} J_i\sigma_i \sigma_{i+1} \right)$$
где – обратная температура.
Спин-спиновая корреляционная функция:
$$G(k,k+r)\equiv<\sigma_k\sigma_{k+r}>=\frac{1}{Z_N}\sum_{\{\sigma\}}\sigma_k \sigma_{k+r} exp\left(\sum_{i=1}^{N-1} \beta J_i\sigma_i\sigma_{i+1} \right)$$
Магнитная восприимчивость вблизи критической температуры TC=0 в нулевом магнитном поле
$$\chi_T\approx\frac{1}{T}e^{2\frac{J}{T}}$$
Теплоемкость вблизи ТС=0 :
$$C_H=-\frac{\partial}{\partial\beta}lnZ_N=-\frac{\partial}{\partial\beta}\left[ln(2^Nch^{N-1}(\beta J)\right]$$
$$C_H=(N-1)[\beta J sch(\beta J)]^2$$
Энтропия:
$$S=\frac{\partial(T lnZ)}{\partial T} = lnZ_N+T\frac{\partial lnZ_N}{\partial T}=Nln2+(N-1)ln[ch(\beta J)-(N-1)\beta Jth(\beta J)]$$
При T \(\rightarrow \infty\), S \(\rightarrow\) Nln2, а при T\(\rightarrow\) 0 получим
$$S\approx ln2+(N+1)ln \left( \frac{2ch(\beta J)}{e^{\beta Jth(\beta J)}
}\right )\approx ln2 + (N-1) ln \left ( \frac{e^{\beta J} + e^{-\beta J}}{e^{\beta J}} \right ) =ln2$$
Рассмотрим невозможность фазового перехода в случае одномерной цепочке спинов. Пусть при некоторой конечной температуре все спины цепочки из N атомов имеют значение si=+1. При перевороте всех спинов цепочки для которых i > k, разрывается лишь одна связь обменного взаимодействия соседних спинов, изменение энергии составляет 2J и не зависит от числа спинов в цепочке. Так как число способов, которыми можно сделать такое разупорядочение, равно N, изменение энтропии равно lnN. Полное изменение свободной энергии
$$\bigtriangleup F=2J-TlnN$$
Для любого значения J при достаточно больших значениях N изменение свободной энергии будет отрицательным. Значит упорядоченное состояние одномерной цепочки является термодинамически неустойчивым.
Аналогично можно продемонстрировать, что для двумерной решетки Изинга должна существовать конечная температура, ниже которой упорядоченное состояние становится термодинамически устойчивым.
Рассмотрим произвольный замкнутый контур, который ограничивает на плоской решетке область спинов одной ориентации (темные шары на рис. 1). Пусть длина этого контура равна L (в единицах расстояний между соседними спинами). Контур пересекает всего L межатомных связей. Изменение обменной энергии на границе контура равно 2J · L, а изменение энтропии пропорционально логарифму числа способов выбора области с данной длиной границы. Так как в каждом узле решетки имеется три варианта выбора направления движения, то число способов выбора такой области пропорционально 3L . Следовательно, изменение свободной энергии решетки
$$\bigtriangleup F\approx 2L-T ln(3^L)=L (2J-Tln3)$$
Свободная энергия превращается в нуль, т.е. происходит магнитный фазовый переход при температуре Tc=2J/ln3
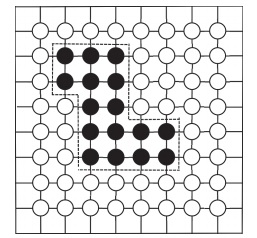
Рис. 1. – Модель двумерной решетки Изинга
Рассмотренный подход дает очень приближенное значение температуры Кюри двумерной решетки Изинга. Точное решение было получено Л. Онсагером в 1944 г. [17]: Вблизи ТС температурный ход намагниченности определяется критической экспонентой β = 1/8, т. е. M~(Tc-T)1/8

