В данном разделе будут рассмотрены: понятие алгоритма, вычислительная сложность алгоритма, а также особенности параллельных вычислений для классических задач.

Среди подходов к реализации параллелизма можно выделить три: ручной, автоматический и модельный. При «ручном проектировании» программист берет на себя всю ответственность за структуру и качество параллельного решения. Используя ту или иную библиотеку (MPI, OPEN МР и т.п.), он создает параллельную программу, самостоятельно формируя ее структуру, связи, синхронизацию и т.д. При автоматическом распараллеливании написанная в обычном стиле программа преобразуется в параллельную без участия программиста. Разумеется, за качество распараллеливания отвечает система или среда программирования. Хорошая программная система может появиться только тогда, когда разум вычислительной системы будет выше человеческого разума. В настоящее время приходится довольствоваться в основном распараллеливанием цикла. В полном объеме эта задача в настоящее время не решена. Модельный подход отличается тем, что в нем есть та или иная формальная основа – универсальная алгоритмическая модель параллельных вычислений.

Таким образом, на сегодня реальным является параллелизм универсальных вычислений и их использование в качестве основных модулей при решении конкретных задач.

Опыт программирования показывает, что точность вычислений часто зависит от их порядка, хотя математически эти операции могут быть выполнены в произвольном порядке. Так, даже для целых чисел результаты вычислений 3/2*6 и 3*6/2 будут разными, в случае чисел с плавающей точкой эти зависимости усиливаются.

 

Понятие алгоритма

Алгоритм – точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Обращаем внимание на слова последовательность действий. Действительно, само понятие алгоритма и его использование практически всегда предполагали последовательные вычисления.

Для того чтобы понятие алгоритма применять для параллельных вычислений, используем определение Т. Кормена. Алгоритм – это формально описанная вычислительная процедура, получающая исходные данные (input), называемые также входом алгоритма или его аргументом, и выдающая результат вычислений на выход (output). Заметим, что здесь ничего не говорится о последовательности действий. В дальнейшем будем рассматривать алгоритм как «черный ящик», выполняющий преобразование входных данных в выходные, эти преобразования могут быть последовательными, параллельными или смешанными.

Основной характеристикой алгоритма является его вычислительная сложность.

 

Понятие вычислительной сложности алгоритма

Пусть А – алгоритм решения некоторого класса задач, например, сортировки. Назовем размерностью задачи \(n\) совокупность параметров (их количество), характеризующих объем обрабатываемых исходных данных и определяющих необходимые для выполнения расчетов ресурсы (время, память). Для задачи сортировки – это тип сортируемых данных и их количество.

Вычислительная сложность алгоритма зависит от размерности задачи и делится на:

• временную сложность;
• пространственную (емкостную) сложность.

Временная сложность определяет время, необходимое для выполнения заданного алгоритма. Пространственная (емкостная) сложность определяет необходимый объем памяти.

Здесь предполагается, что вычислительная сложность – это временная сложность. Если понятие вычислительной сложности будет предполагать использование пространственной сложности, будет оговорено.

 

Граф параллельного алгоритма

Современный процессор выполняет операции не в том порядке, в котором они заданы в программе, а в том порядке, в котором они могут быть выполнены. При этом обеспечивается максимальная загрузка всех блоков процессора. Так, для вычисления известной из школы формулы: $$S=\sqrt{p(p-a)(p-b)(p-c)} $$операции \(р–а, р–b, р–с\) можно выполнить параллельно, затем параллельно вычислить подкоренное выражение и, наконец, сам корень (рис. 2).

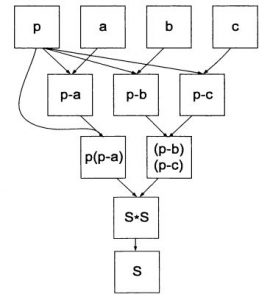
Рис. 2. Граф параллельного алгоритма вычисления площади треугольника

Данный граф является однонаправленным. Высота графа определяет минимальное число операций, за которые можно выполнить задачу при параллельных вычислениях. Для данной задачи высота графа равна 4, т.е. для вычислений требуется минимум 4 операции.

Степень параллелизма для данного этапа – количество операций, которое можно выполнить параллельно.

Средняя степень параллелизма определяется как отношение общего числа операций, которые надо выполнить, на число этапов, за которые эти операции выполняются. Для нашего примера общее число операций равно 7, а число шагов равно 4, средняя степень параллелизма равна 1.75. В отличие от ускорения, эта характеристика никак не зависит от числа ядер процессора и характеризует только алгоритм.

Параллельные алгоритмы вычисления суммы

Пусть необходимо вычислить значение суммы:

$$\sum_{i=0}^{i=n-1} x_{i}$$

Рассмотрим фрагмент программы для вычисления суммы классическим последовательным способом:

for (int i = 0, s = 0; i < n; ++i)
s += a [i];

 

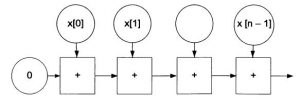
Рис. 3. Граф для последовательного вычисления суммы

Очевидно, что, независимо от числа ядер, данный алгоритм требует последовательного выполнения n операций сложения и сравнения. Граф в данном случае (рис. 3) выглядит как непрерывная линейная цепочка, степень параллелизма совпадает со средней степенью параллелизма и равна 1.

Каскадный метод вычисления суммы

Пусть есть бесконечное число вычислительных блоков (ядер). В этом случае для каждой пары слагаемых вычисляем сумму параллельно (предполагается, что все слагаемые предварительно вычислены и доступны вычислительному блоку):

for (int i = 0, j = 0; i < n; i +=2, ++j)
b[j] = a[2 * i] + a [2 * i+l];

Для \(n/2\) процессоров все элементы \(b[j]\) могут быть вычислены параллельно.

Далее, для полученых частичных сумм вычисляем сумму:

for (int i = 0, j = 0; i < n /2; i +=2, ++j)
b[j] = b[2 *i] + b [2 * i+1];

и т.д.

Программная реализация каскадного метода для последовательного режима:

//Каскадный метод
int CascadeSumma (const int *x, size_t n)
{
int у [MAXSIZE];
memcpy (y, x,n* sizeof (int));
while (n >=2)
{
n/=2;
for (size_tj = 0; j < n; ++j)
y[j] = y[2*j] + y[2*j+ 1];
}
return у [0];
}

Так как сумма элементов с четным и нечетным номером может выполняться параллельно для всех пар, то в графе на первом шаге получим \(n/2\) вершин. Каждый очередной шаг приводит к уменьшению числа вершин в 2 раза. Граф для 8-ми слагаемых представлен на рис. 4.

Очевидно, что каскадный метод требует  шагов при условии наличия \(n/2\) ядер процессора.

Определим степень параллелизма алгоритма:

Шаг 1: \(n/2\)

Шаг 2: \(n/4\)

Шаг \(log_{2}n\):  1

Средняя степень параллелизма равна \(S = n/(log_{2}n)\) .

Определим показатели ускорения, эффективности и стоимости для каскадного метода.

\(S=T_{посл}/T_{парал}=n/log_{2}n\) ; \(Е = S/(n/2) – 2S/n\); \(C =log_{2}n * n/2\)

Заметим, что средняя степень параллелизма совпадает с ускорением при условии наличия максимального необходимого числа ядер. При \( n \rightarrow \infty\) эффективность \( E \rightarrow \infty\).

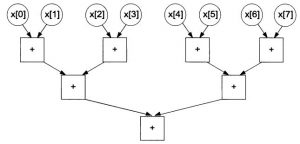
Рис. 4. Граф для параллельного сложения 8-ми чисел

Реализация каскадного метода в параллельном режиме имеет смысл только для \(n/2\) ядер.

Комбинированный метод

Пусть число процессоров равно \(p(p < n/2)\)

Разделим n слагаемых на р порций, каждая порция будет содержать \((n+p–1)/р\) элементов. Для упрощения вычислений предположим, что \(n\) кратно \(p\), если это не так, исходный массив всегда можно дополнить нулевыми элементами. Тогда число элементов в порции равно \(n/p\). В каждой порции будем считать сумму традиционным последовательным методом. Вычисления для одной порции делает одно ядро, поэтому эти вычисления могут выполняться параллельно. После вычисления \(p\) частичных сумм определяем сумму, используя каскадный метод.

Граф для комбинированного метода представлен на рис. 5. В этом графе предполагается, что число слагаемых равно 8, а число ядер процессора – 2.

В этом случае время параллельных вычислений составляет:

\[T_{парал}=n/p+log_{2}p\]

Это же высота графа. Степень параллелизма на шаге 1 равна \(р\), на последующих шагах \(p/2, p/4,…, 1\). Таким образом, степени параллелизма образуют убывающую геометрическую прогрессию со знаменателем 0.5. Средняя степень параллелизма равна:

\[\frac{1}{log_{2}p+1}*p*\frac{1-(0,5)^{(log_{2}p+1)}}{1-0,5}\]

В этой формуле число членов прогрессии равно \(log_{2}p +1\). Для получения данной формулы  используется формула для вычисления значения n-ого члена прогрессии \(b_1\frac{1-q^n}{1-q}\). Определим значение средней степени параллелизма для графа на рис. 5. На первом шаге степень параллелизма равна 2, на втором 1, среднее значение равно 1.5. Для приведенной выше формулы получаем при \(р = 2\) значение 1.5.

Определим показатели ускорения, эффективности и стоимости для комбинированного метода.

\[S=T_{посл}/T_{парал}=n/(n/p+log_{2}(p)\];

\[Е = S/p\];

\[С =T_{парал}*p\];

Ниже представлены графики изменения ускорения (рис. 6а) и эффективности (рис. 6б) в зависимости от числа слагаемых для каскадного (Ряд 1) и комбинированного (Ряд 2) метода.

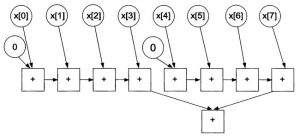
Рис. 5. Граф комбинированной схемы

Из графиков следует, что для каскадного метода ускорение растет с увеличением числа слагаемых, но медленнее, чем число необходимых ядер процессора. Так, для числа слагаемых 512 требуется 256 ядер, и ускорение составляет приблизительно 57, а для числа слагаемых 8192 число ядер равно 4096, а ускорение составляет 630. Таким образом, увеличение числа слагаемых в 16 раз приводит к увеличению ускорения в 11 раз. Изменение скорости роста фактически отражает показатель эффективности, который падает с увеличением числа слагаемых. Для комбинированного метода эффективность растет. Кроме того, с помощью комбинированного метода можно решить задачу с любым числом ядер и числом слагаемых. Для каскадного метода требуется число ядер, которое на сегодня является нереальным.

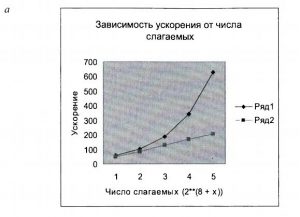
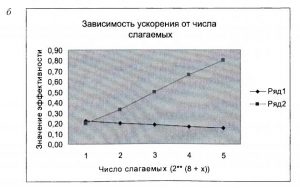
Рис. 6. Зависимость ускорения и эффективности для каскадного и комбинированного методов вычисления суммы

Заметим, что этот же принцип вычисления можно использовать для вычисления произведения элементов массива, минимального и максимального элементов.

 Вычисление частичных сумм

Пусть необходимо вычислить:

\[S_{i}=\sum_{i=0}^{i=n-1} x_{i}\]

В последовательном режиме для решения этой задачи необходимо выполнить такое же число операций, как для вычисления согласно (2), т.е. \(n–1\) операций.

Каскадный метод в чистом виде для решения этой задачи неприменим. Модифицируем этот метод:

В качестве начального значения \(S_{i}\) присвоим значение i-го слагаемого \(x_{i}\) .

Шаг 1. Сдвинем массив \(S\)  на 1 элемент вправо. Свободный элемент слева сделаем равным 0, последний элемент массива \(х\) теряется. Выполним покомпонентное суммирование элементов массива \(S\) их. В результате получим значения:

В результате выполнения первого шага получаем правильные значения \(S_{0}-S_{1}\). Остальные значения необходимо дополнять. Для выполнения шага 1 при наличии n ядер требуется одна операция, включающая в себя сдвиг и сложение.

Шаг 2. Вычисляем значение \(S = (S>>2) + S\)

В результате выполнения шага 2 получили правильные значения \(S_{0}-S_{3}\) . Для выполнения шага 2 при наличии \(n\) ядер требуется одна операция, включающая в себя сдвиг и сложение.

Шаг 3. Вычисляем значение \(S = (S>>4) + S\):

В результате выполнения шага 3 получили все правильные значения \(S\). Для выполнения шага 3 при наличии \(n\) ядер требуется одна операция, включающая в себя сдвиг и сложение. Граф для вычисления частичных сумм для массива с 8-ми элементами представлен на рис. 6.

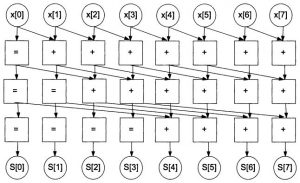
Рис. 6. Параллельный алгоритм вычисления частичных сумм

Таким образом, общее число шагов для восьми слагаемых равно \(log_{2}n\) (высота графа). Степень параллелизма на каждом шаге равна числу элементов массива \(n\).

Общий вид алгоритма:

//копирование массива
S=x;
for (step = 0; step < (n); step++)
{
ShiftConst= 1<<step;
for (i = ShiftConst; i < n; i++)
S[i] += S[i- ShiftConst];
}

Все итерации цикла по i независимы, шаги необходимо выполнять последовательно, переход на очередной шаг допустим после полного завершения предыдущего шага.

Можно считать, что в цикле для каждого шага необходимо выполнить 2 операции: вычисление константы сдвига и параллельное вычисление новых значений элементов массива \(S[i]\), в этом случае общее количество операций для каскадного метода составляет \(2*log_{2}n\) Определим показатели ускорения и эффективности:

\(S=n/(2* log_{2}n)\);

\(E= 1/(2*log_{2}n)\) .

Для рассмотренного алгоритма требуется процессор с \(n\) ядрами. Для уменьшения числа необходимых ядер внутренний цикл можно считать параллельно-последовательно, определив число порций по количеству доступных ядер. Каждая порция выполняется последовательно.

Заметим, что выигрыш получаем только при \(n > 4\), реализация алгоритма в случае двух потоков не имеет смысла, так как эта реализация будет сложнее, чем для алгоритма вычисления обычной суммы, а для последнего алгоритма мы не получили выигрыша.

1. Алгоритм сложения [Электронный ресурс]: Режим доступа:
   http://www.intuit.ru/department/supercomputing/inparllalg/class/free/status
2. Качко, Е.Г. Параллельное программирование: Учебное пособие / Е.Г. Качко. –
   Харьков:Изд-во «Форт», 2011. – 528 с.
3. Параллелизм [Электронный ресурс]: Режим доступа:
   http://www.osp.ru/text/print/302/4569688.html